本篇文章给大家带来了关于mysql中索引底层以及优化的相关知识,下面我们就整理一下mysql中索引的知识点,希望对大家有帮助。

Mysql索引篇
最近在很多网站上看了索引的相关知识,各种说法的都有,但是又不是很全,有的概念很模糊,下面是由小编整理的Mysql索引知识点。
一.首先我们说下什么是索引,为什么要用索引
索引用于快速找出在某个列中有一特定值的行,不使用索引,MySQL必须从第一条记录开始读完整个表,直到找出相关的行,表越大,查询数据所花费的时间就越多,如果表中查询的列有一个索引,MySQL能够快速到达一个位置去搜索数据文件,而不必查看所有数据,那么将会节省很大一部分时间。
二. 索引类型分为两类:
1.hash索引
2.bTree
三.下面我们简单分析一下hash索引和bTree索引。
1. 哈希表是一种以键 – 值(key-value)存储数据的结构,我们只要输入待查找的键即 key,就可以找到其对应的值即 Value。哈希的思路很简单,把值放在数组里,用一个哈希函数把 key 换算成一个确定的位置,然后把 value 放在数组的这个位置。
不可避免地,多个 key 值经过哈希函数的换算,会出现同一个值的情况。处理这种情况的一种方法是,拉出一个链表。
2. 说到bTree,就不得不提二叉树,二叉树分为很多,例:二叉查找树,平衡二叉树等。当然还有重点红黑树。
1) 二叉查找树的特点是: 父节点左子树所有节点的值小于父节点的值。右子树所有节点的值大于父节点的值。 下面以一张图为例来体现二叉查找树。
| ID | name |
|---|---|
| 5 | 张五 |
| 6 | 张六 |
| 7 | 张七 |
| 2 | 张二 |
| 1 | 张一 |
| 4 | 张四 |
| 3 | 张三 |
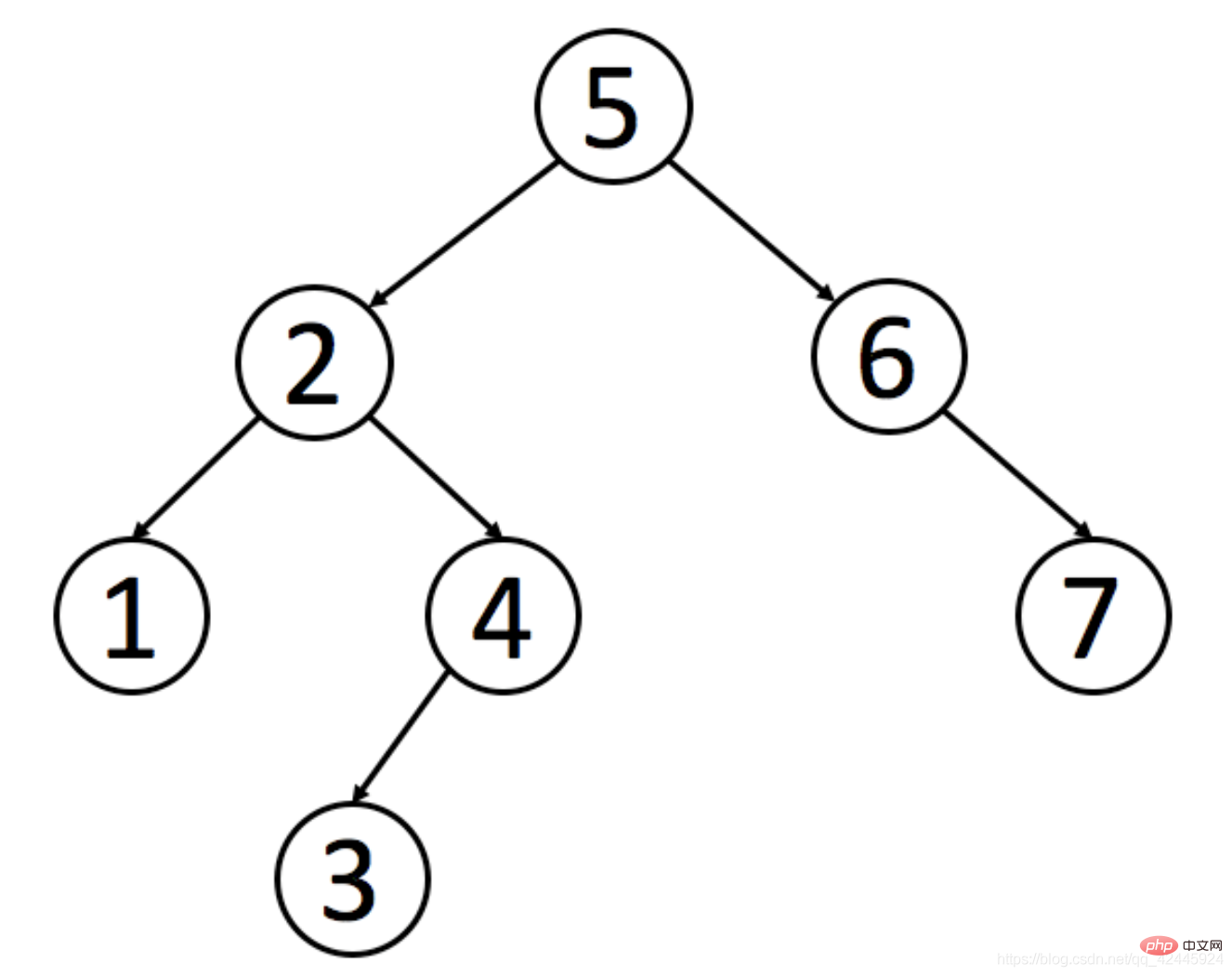 有一个需求,查找张三,如果不使用二叉查找树那么我们需要查找7次,使用二叉查找树我们只需要查找4次就可以找到我们想要的值。
有一个需求,查找张三,如果不使用二叉查找树那么我们需要查找7次,使用二叉查找树我们只需要查找4次就可以找到我们想要的值。
根据上面说的使用二叉查找树的确可以减少查询次数,但是大家有没有想过,如果数据库的数据是 1,2,3,4,5,6,7这样依次递增的数据呢,继续使用二叉查找树就会变成一个链表了。那这样如果我们想要查找7那么需要查找7次,扫描表也是需要7次。这样跟没有建立索引没有区别,这也是弊端之一。下图为例说明。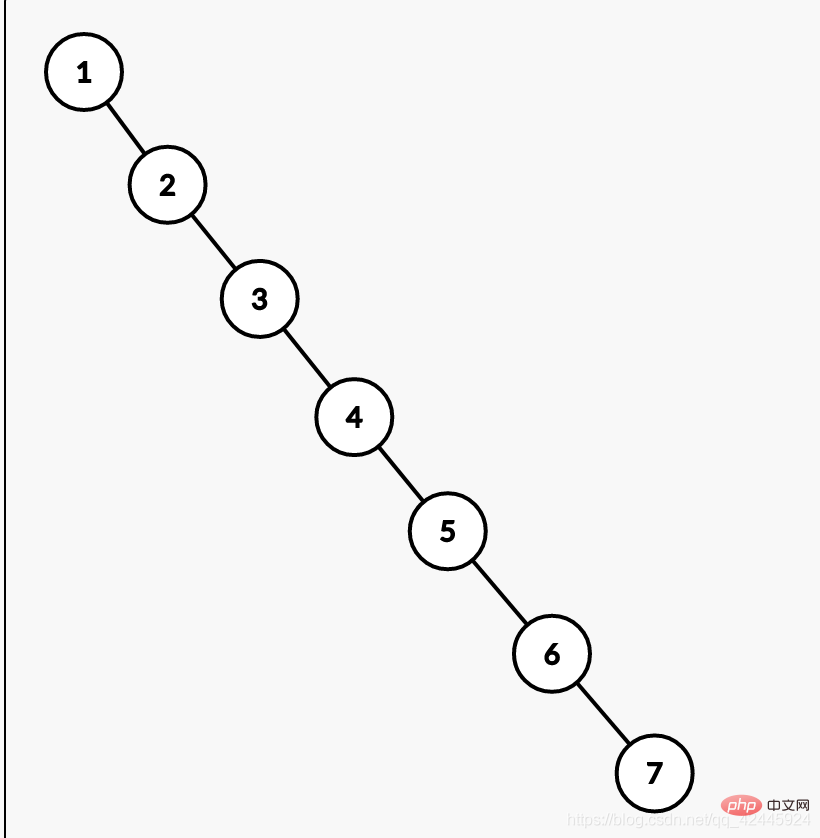
2) 平衡二叉树:又被称为AVL树,它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树,AVL树是最早发明的自平衡二叉查找树。在AVL树中,任何节点的两个子树的高度最大差别只能为1,所以它又被称为高度平衡树。查询、增加和删除在平均和最坏情况下都是O(log n)。增加和删除会需要通过一次或多次树旋转来重新平衡这个树。
我们引入二叉树的目的是为了提高二叉树的搜索的效率,从而减少树的平均搜索长度,为此,就必须在每颗二叉树插入一个结点时调整树的结构,让二叉树搜索能够保持平衡,从而可能降低树的高度,减少的平均树的搜索长度。
平衡二叉树特点如下:
1.它的左子树和右子树都是AVL树
2.左子树和右子树的高度差不能超过1
例图: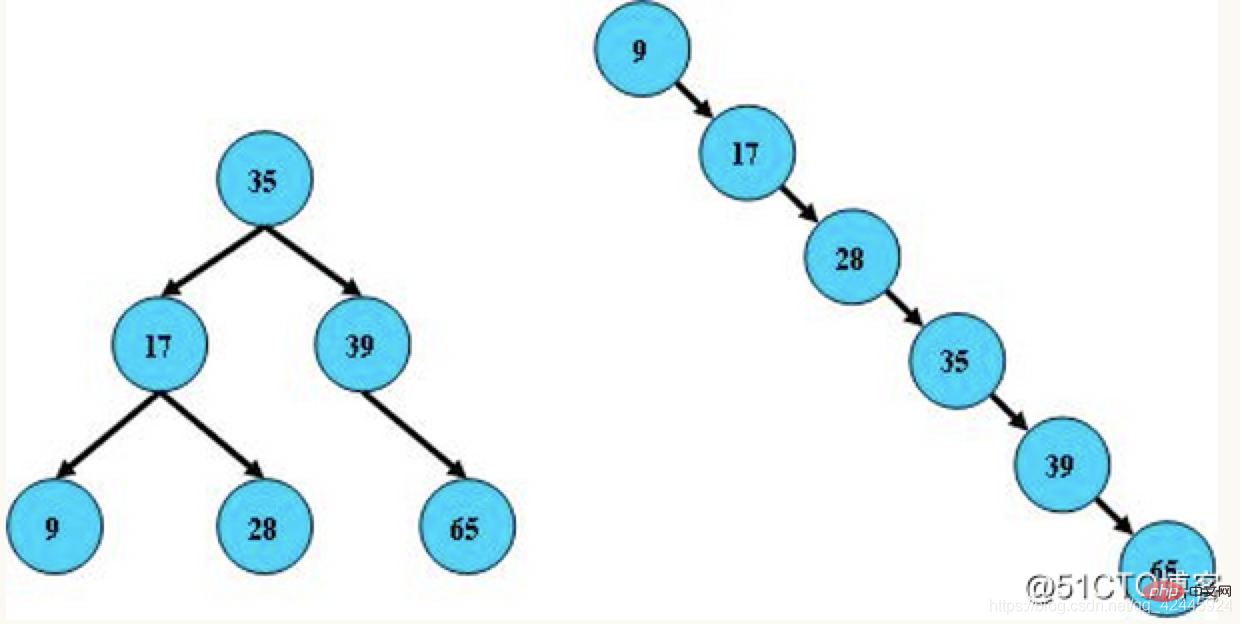 3) 红黑树:可以理解为红黑树是凌驾于平衡二叉树之上的一棵树,红黑树不会追求“完全平衡 ”,它只会求部分达到平衡要求,降低了对旋转的要求,从而提高性能。此外,由于它的设计,所有不平衡都能够在三次旋转之内解决。在红黑树中,它的算法时间复杂度与AVL相同,并且统计性能会逼AVL树更高。所以红黑树相对于平衡二叉树来说,不是严格意义上的平衡二叉树,红黑树插入和删除效率更高一些,查询的效率比平衡二叉树来说相对低一些,但是二者查询效率差值做对比,基本可以忽略不计。红黑树特点如下:
3) 红黑树:可以理解为红黑树是凌驾于平衡二叉树之上的一棵树,红黑树不会追求“完全平衡 ”,它只会求部分达到平衡要求,降低了对旋转的要求,从而提高性能。此外,由于它的设计,所有不平衡都能够在三次旋转之内解决。在红黑树中,它的算法时间复杂度与AVL相同,并且统计性能会逼AVL树更高。所以红黑树相对于平衡二叉树来说,不是严格意义上的平衡二叉树,红黑树插入和删除效率更高一些,查询的效率比平衡二叉树来说相对低一些,但是二者查询效率差值做对比,基本可以忽略不计。红黑树特点如下:
1. 节点是红色或黑色。
2. 根节点是黑色。
3. 每个红色节点的两个子节点都是黑色。(红色节点的子节点必须是黑色节点)
4. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
故红黑树是黑色平衡的树,左子树与右子树高度差不会超过2。红节点的父节点、子节点只能是黑节点。
例图: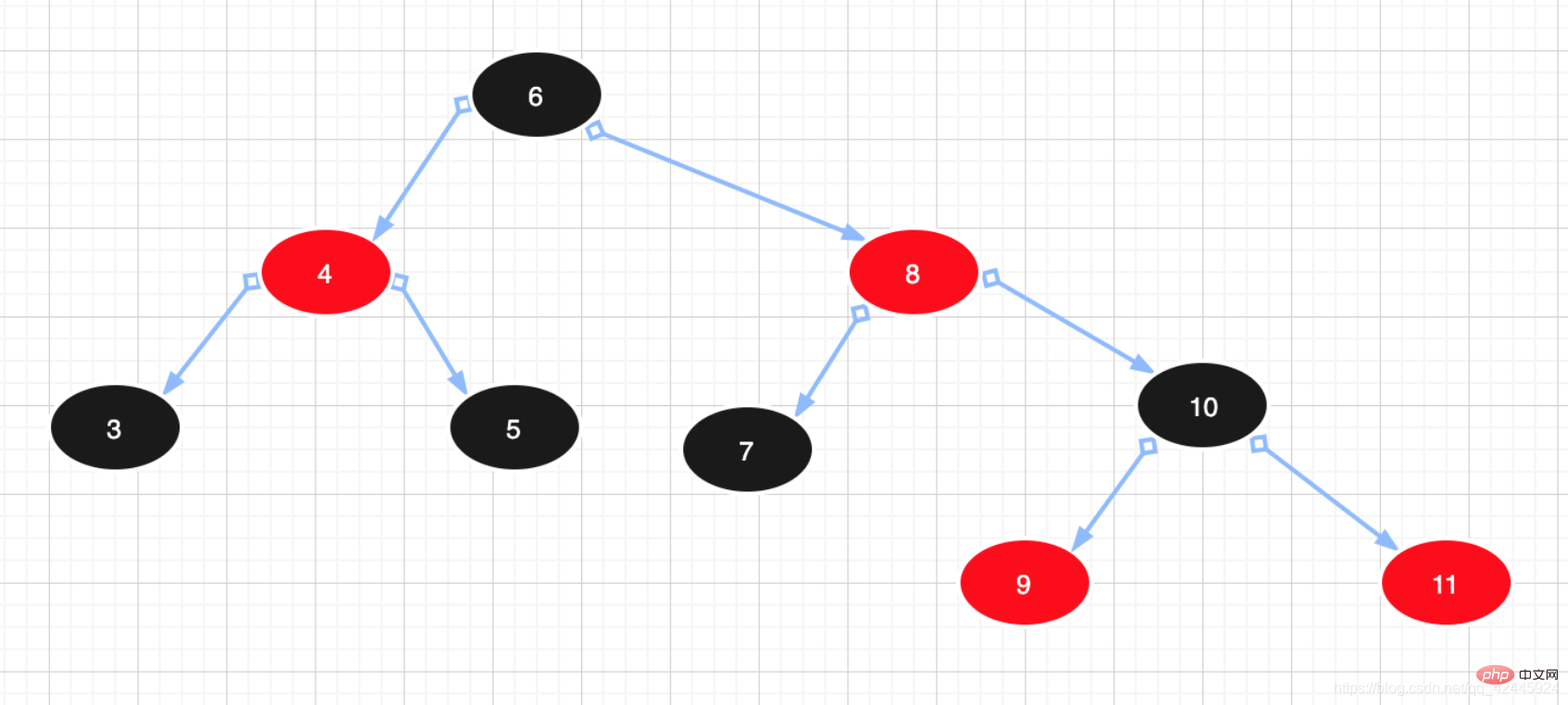
4) BTree(B树):当然上面说到了红黑树,性能非常高。以上图为例,树的高度最高才为4,共9条数据,但是对于Mysql数据库,动则几百万条数据,几千万条数据,那树的高度就不可估量了,比如说上百万条数据需要经过30-50次磁盘IO才能查询到数据,甚至
 站长资讯网
站长资讯网