冒泡排序、快速排序和堆排序的时间复杂度是多少

冒泡排序的时间复杂度：最好情况是“O(n)”，最坏情况是“O(n2)”。快速排序的的时间复杂度：最好情况是“O(nlogn)”，最坏情况是“O(n2)”。堆排序的时间复杂度是“O(nlogn)”。

本教程操作环境：windows7系统、Dell G3电脑。

冒泡排序（Bubble Sort）

时间复杂度

最好的情况：数组本身是顺序的，外层循环遍历一次就完成O(n)

最坏的情况：数组本身是逆序的，内外层遍历O(n2)

空间复杂度
开辟一个空间交换顺序O(1)
稳定性
稳定，因为if判断不成立，就不会交换顺序，不会交换相同元素

• 冒泡排序它在所有排序算法中最简单。然而， 从运行时间的角度来看，冒泡排序是最差的一个，它的复杂度是O(n2)。

• 冒泡排序比较任何两个相邻的项，如果第一个比第二个大，则交换它们。元素项向上移动至正确的顺序，就好像气泡升至表面一样，冒泡排序因此得名。

• 交换时，我们用一个中间值来存储某一交换项的值。其他排序法也会用到这个方法，因此我 们声明一个方法放置这段交换代码以便重用。使用ES6（ECMAScript 2015）**增强的对象属性——对象数组的解构赋值语法，**这个函数可以写成下面 这样：

[array[index1], array[index2]] = [array[index2], array[index1]];

具体实现：

function bubbleSort(arr) {   for (let i = 0; i < arr.length; i++) {//外循环（行{2}）会从数组的第一位迭代 至最后一位，它控制了在数组中经过多少轮排序     for (let j = 0; j < arr.length - i; j++) {//内循环将从第一位迭代至length - i位，因为后i位已经是排好序的，不用重新迭代       if (arr[j] > arr[j + 1]) {//如果前一位大于后一位         [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];//交换位置       }     }   }   return arr; }

快速排序

时间复杂度
最好的情况：每一次base值都刚好平分整个数组，O(nlogn)
最坏的情况：每一次base值都是数组中的最大/最小值，O(n2)

空间复杂度
快速排序是递归的，需要借助栈来保存每一层递归的调用信息，所以空间复杂度和递归树的深度一致
最好的情况：每一次base值都刚好平分整个数组，递归树的深度O(logn)
最坏的情况：每一次base值都是数组中的最大/最小值，递归树的深度O(n)

稳定性
快速排序是不稳定的，因为可能会交换相同的关键字。
快速排序是递归的，
特殊情况：left>right,直接退出。

步骤：

(1) 首先，从数组中选择中间一项作为主元base，一般取第一个值。

(2) 创建两个指针，左边一个指向数组第一个项，右边一个指向数组最后一个项。移动右指针直到找到一个比主元小的元素，接着，移动左指 针直到我们找到一个比主元大的元素，然后交 换它们，重复这个过程，直到左指针遇见了右指针。这个过程将使得比主元小的值都排在主元之前，而比主元大的值都排在主元之后。这一步叫作划分操作。

(3)然后交换主元和指针停下来的位置的元素（等于说是把这个元素归位，这个元素左边的都比他小，右边的都比他大，这个位置就是他最终的位置）

(4) 接着，算法对划分后的小数组（较主元小的值组成的子数组，以及较主元大的值组成的 子数组）重复之前的两个步骤(递归方法），

递归的出口为left/right=i，也就是：

left>i-1 / i+1>right

此时，子数组数组已排序完成。

归位示意图：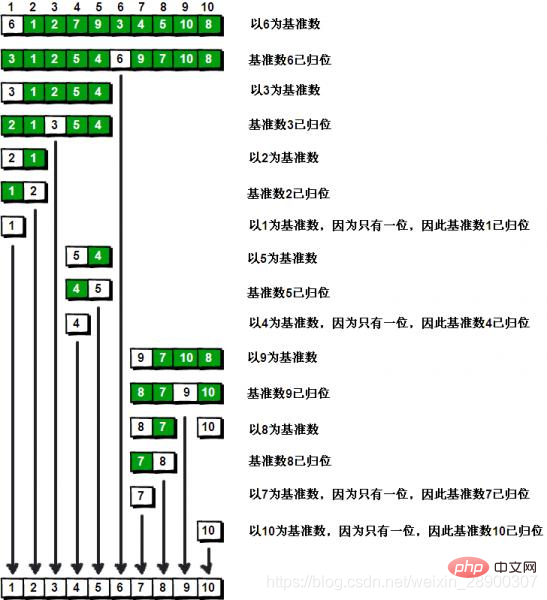

具体实现：

function quicksort(arr, left, right) {   if (left > right) {     return;   }   var i = left,     j = right,     base = arr[left]; //基准总是取序列开头的元素   //   var [base, i, j] = [arr[left], left, right]; //以left指针元素为base   while (i != j) {     //i=j，两个指针相遇时，一次排序完成，跳出循环     // 因为每次大循环里面的操作都会改变i和j的值，所以每次循环/操作前都要判断是否满足i<j     while (i < j && arr[j] >= base) {       //寻找小于base的右指针元素a，跳出循环，否则左移一位       j--;     }     while (i < j && arr[i] <= base) {       //寻找大于base的左指针元素b，跳出循环，否则右移一位       i++;     }     if (i < j) {       [arr[i], arr[j]] = [arr[j], arr[i]]; //交换a和b     }   }   [arr[left], arr[j]] = [arr[j], arr[left]]; //交换相遇位置元素和base，base归位   //   let k = i;   quicksort(arr, left, i - 1); //对base左边的元素递归排序   quicksort(arr, i + 1, right); //对base右边的元素递归排序   return arr; }

参考：https://www.cnblogs.com/venoral/p/5180439.html

堆排序

堆的概念

• 堆是一个完全二叉树。
• 完全二叉树： 二叉树除开最后一层，其他层结点数都达到最大，最后一层的所有结点都集中在左边（左边结点排列满的情况下，右边才能缺失结点）。
• 大顶堆：根结点为最大值，每个结点的值大于或等于其孩子结点的值。
• 小顶堆：根结点为最小值，每个结点的值小于或等于其孩子结点的值。
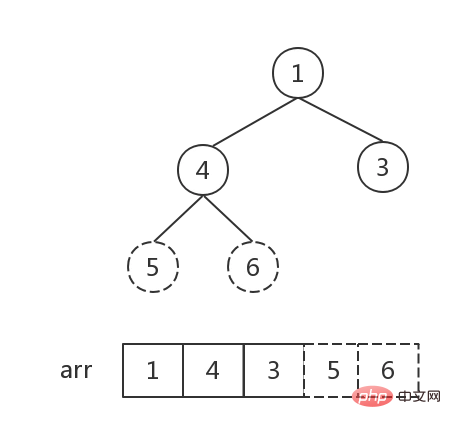
• 堆的存储： 堆由数组来实现，相当于对二叉树做层序遍历。如下图：
  
  

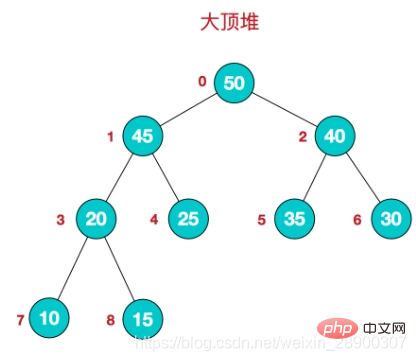
时间复杂度
总时间为建堆时间+n次调整堆 —— O(n)+O(nlogn)=O(nlogn)
建堆时间：从最后一个非叶子节点遍历到根节点，复杂度为O(n)
n次调整堆：每一次调整堆最长的路径是从树的根节点到叶子结点，也就是树的高度logn，所以每一次调整时间复杂度是O(logn)，一共是O(nlogn)

空间复杂度
堆排序只需要在交换元素的时候申请一个空间暂存元素，其他操作都是在原数组操作，空间复杂度为O(1)

稳定性
堆排序是不稳定的，因为可能会交换相同的子结点。

步骤一：建堆

• 以升序遍历为例子，需要先将将初始二叉树转换成大顶堆，要求满足：树中任一非叶子结点大于其左右孩子。
• 实质上是调整数组元素的位置，不断比较，做交换操作。
• 找到第一个非叶子结点——Math.floor(arr.length / 2 - 1)，从后往前依次遍历
• 对每一个结点，检查结点和子结点的大小关系，调整成大根堆

// 建立大顶堆 function buildHeap(arr) {   //从最后一个非叶子节点开始，向前遍历，   for (let i = Math.floor(arr.length / 2 - 1); i >= 0; i--) {     headAdjust(arr, i, arr.length); //对每一个节点都调整堆，使其满足大顶堆规则   } }

步骤二：调整指定结点形成大根堆

• 建立childMax指针指向child最大值节点，初始值为2 * cur + 1，指向左节点
• 当左节点存在时（左节点索引小于数组length），进入循环，递归调整所有节点位置，直到没有左节点为止（cur指向一个叶结点为止），跳出循环，遍历结束
• 每次循环，先判断右节点存在时，右节点是否大于左节点，是则改变childMax的指向
• 然后判断cur根节点是否大于childMax，
• 大于的话，说明满足大顶堆规律，不需要再调整，跳出循环，结束遍历
• 小于的话，说明不满足大顶堆规律，交换根节点和子结点，
• 因为交换了节点位置，子结点可能会不满足大顶堆顺序，所以还要判断子结点然后，改变cur和childMax指向子结点，继续循环判断。

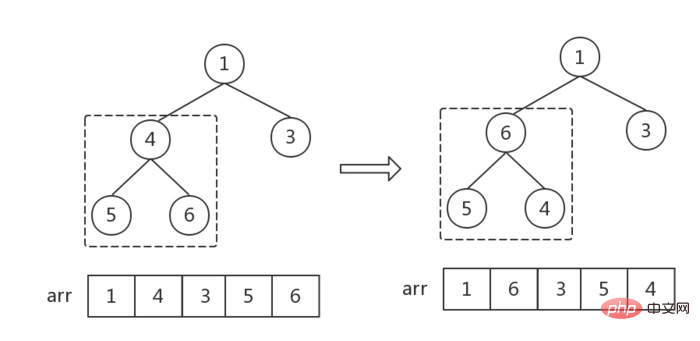
//从输入节点处调整堆 function headAdjust(arr, cur, len) {   let intialCur = arr[cur]; //存放最初始的   let childMax = 2 * cur + 1; //指向子树中较大的位置，初始值为左子树的索引    //子树存在（索引没超过数组长度）而且子树值大于根时，此时不符合大顶堆结构，进入循环，调整堆的结构   while (childMax < len) {     //判断左右子树大小,如果右子树更大，而且右子树存在，childMax指针指向右子树     if (arr[childMax] < arr[childMax + 1] && childMax + 1 < len) childMax++;     //子树值小于根节点，不需要调整，退出循环     if (arr[childMax] < arr[cur]) break;     //子树值大于根节点，需要调整，先交换根节点和子节点     swap(arr, childMax, cur);     cur = childMax; //根节点指针指向子节点，检查子节点是否满足大顶堆规则     childMax = 2 * cur + 1; //子节点指针指向新的子节点   } }

步骤三：利用堆进行排序

• 从后往前遍历大顶堆（数组），交换堆顶元素a[0]和当前元素a[i]的位置，将最大值依次放入数组末尾。
• 每交换一次，就要重新调整一下堆，从根节点开始，调整根节点～i-1个节点（数组长度为i），重新生成大顶堆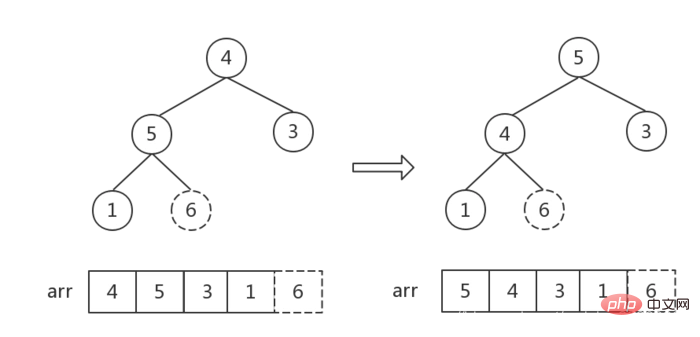
  
  

// 堆排序 function heapSort(arr) {   if (arr.length <= 1) return arr;   //构建大顶堆   buildHeap(arr);   //从后往前遍历，   for (let i = arr.length - 1; i >= 0; i--) {     swap(arr, i, 0); //交换最后位置和第一个位置（堆顶最大值）的位置     headAdjust(arr, 0, i); //调整根节点～i-1个节点，重新生成大顶堆   }   return arr; }

完整代码：

// 交换数组元素 function swap(a, i, j) {   [a[i], a[j]] = [a[j], a[i]]; } //从输入节点处调整堆 function headAdjust(arr, cur, len) {   let intialCur = arr[cur]; //存放最初始的   let childMax = 2 * cur + 1; //指向子树中较大的位置，初始值为左子树的索引    //子树存在（索引没超过数组长度）而且子树值大于根时，此时不符合大顶堆结构，进入循环，调整堆的结构   while (childMax < len) {     //判断左右子树大小,如果右子树更大，而且右子树存在，childMax指针指向右子树     if (arr[childMax] < arr[childMax + 1] && childMax + 1 < len) childMax++;     //子树值小于根节点，不需要调整，退出循环     if (arr[childMax] < arr[cur]) break;     //子树值大于根节点，需要调整，先交换根节点和子节点     swap(arr, childMax, cur);     cur = childMax; //根节点指针指向子节点，检查子节点是否满足大顶堆规则     childMax = 2 * cur + 1; //子节点指针指向新的子节点   } } // 建立大顶堆 function buildHeap(arr) {   //从最后一个非叶子节点开始，向前遍历，   for (let i = Math.floor(arr.length / 2 - 1); i >= 0; i--) {     headAdjust(arr, i, arr.length); //对每一个节点都调整堆，使其满足大顶堆规则   } } // 堆排序 function heapSort(arr) {   if (arr.length <= 1) return arr;   //构建大顶堆   buildHeap(arr);   //从后往前遍历，   for (let i = arr.length - 1; i >= 0; i--) {     swap(arr, i, 0); //交换最后位置和第一个位置（堆顶最大值）的位置     headAdjust(arr, 0, i); //调整根节点～i-1个节点，重新生成大顶堆   }   return arr; }